Hi, all! Happy holidays and happy New Year!
In the Blog thus far, the discussion has been focused on qubit basics and technology/coursework, admittedly, oriented to the IBM approach: gate-model quantum computing, which seeks to leverage qubit states (0, 1, or a superposition of those values) conceptually in a similar way to classical logic/bit gates that implement a computationally intensive formula or algorithm to achieve a numerical result. Such use case examples include Shor’s algorithm, for prime number factorization, or Grover’s algorithm.
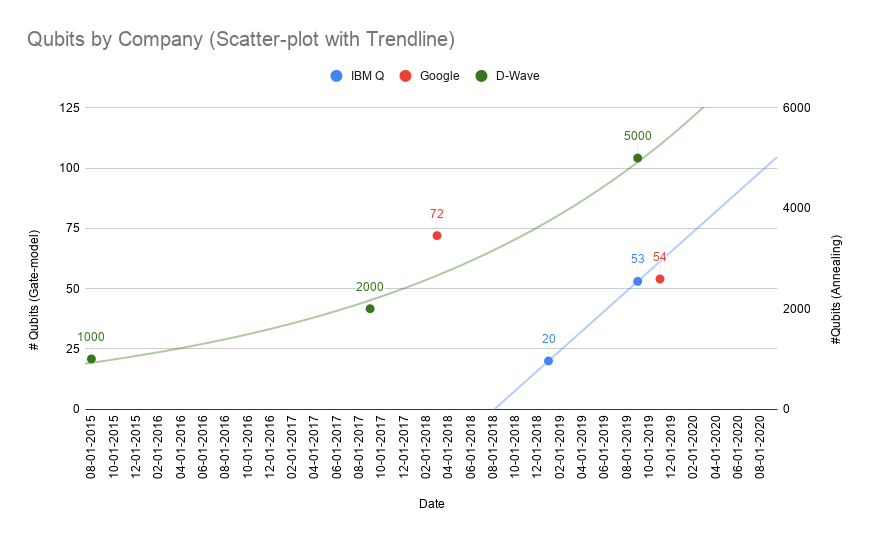
Gate-model quantum computing; however, is only one approach. We have yet to discuss quantum annealing, which uses an approach of measuring energy states to solve optimization use cases such as a molecular/protein modeling and the traveling salesman. Quantum annealing has been in use longer, most prominently by D-wave Systems who has had a number of system announcements dating back to a 1,000 qubit system circa 2015. Thus far with IBM Q and comparable gate model systems we’ve been talking about computation on the order of 50 qubits and quantum advantage occurring theoretically in the 50-100 qubit range (we’re not there yet), but clearly a different order of magnitude with the annealing approach.
Let’s take a second look at our qubit release chart with D-Wave applied. Note trend lines are applied here for IBM Q (left y-axis) and D-Wave (right y-axis). D-Wave has been on an exponential pace for adding qubits. With only a year or so of data for so-called noisy intermediate scale quantum (“NISC”) computers leveraging the gate-model approach, it’s not immediately obvious what the future development pace will be.
So what is quantum annealing? While there are numerous explanations online, I’ll give my own explanation with the intent of practice in mind. Earlier I described annealing as an approach of measuring energy-levels of qubits rather than a pure logical state measurement. Such “energy-level” measurement, or more specifically energy minimization, seems to be the most common description; however, I like to think of the concept as a fancy way of describing good ‘ole maxima/minima determination from classic calculus, just applied to a qubit architecture.
“Wait…calculus?! Ugh.” Yah, sorry. Here’s a reminder image from mathisfun.com (See! Math is Fun!). One use case of derivatives is to find maximum and minimum points in a function, where such points tend to represent a key transition point of the function. A similar technique is used in so-called “Gradient Descent” in many of today’s AI/ML learning algorithms.
In the case of quantum annealing, the solution to an optimization problem is represented by the lowest point of energy, or ground state, in the system. The energy function itself is known as the system “Hamiltonian” and is derived from the interconnected relationship of the qubits. In the case of D-Wave systems, this could be upwards of 5,000 qubits in their latest 5th generation release. Note: there is a wealth of information on Hamiltonian concepts available online; however, I will treat as out of scope here.
Here‘s an example of one of many online visualizations of quantum annealing showing the value of the Hamiltonian as a function over time, including points of minimum energy (local and global Minima values).
In an annealing algorithm, all qubits are set to an initialized state, typically a neutral or x-axis oriented state comparable to the effect of a system of Hadamard gates setting all qubits to a superposition state. Then, by modifying the energy state of an initial set of qubits in the system as a trigger, over time the relationships of the individual qubits drive the entirety of the system to converge towards a respective maximum (“peak”) or minimum (“valley”) states. The system could also diverge to an excited state. Along the way each qubit is measured for it’s state, whether 0 or 1 or superposition, and summed to achieve the total energy value. Upon repeating this process multiple times, the lowest measured state (“global minima”) is said to be the ground state – the solution (or >a< solution) to the problem.
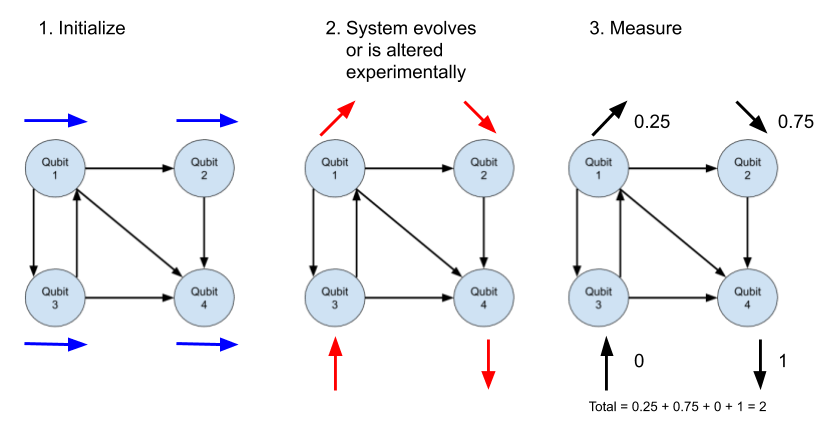
Here’s a visualization of the algorithm above from a topological point of view. Assume a vertical spin upward is a value of ‘0’, a spin downward as a value of ‘1’, and a horizontal spin in the middle as a superposition of the two as an initial state (this is consistent with a qubit modeled as a Bloch sphere). The lines simply represent relationships or couplings between qubits, as defined by the Hamiltonian. In this case the sample represents a measurement of ‘2’; however, this is only a point in time measurement. Over the current pass and subsequent test cases, the energies may be altered differently in Step 2 in which case a lower total energy state (“global minima”) might be found.
One could only imagine the interconnection relationship of a 5,000 D-Wave qubit system, likely being wildly complex, and illustrating the permutations that would make an optimization problem impossible by a classical computer.
One additional topic, a key concept in quantum computing, is quantum tunneling, which is illustrated in the (2x) previous diagram showing a quantum system Hamiltonian progressing over time. In quantum tunneling, the qubit state “tunnels,” conceptually it jumps, through an energy barrier to reach a lower energy state. The best visual I could think of is…a video game reference – ever seen those critters in Dig Dug transform into ghostly eyeballs and mystically traversing through the barriers of dirt?? (advance to :31)
Now, in contrast to tunneling, imagine trying to travel OVER a hill (a “peak”) – a certain amount of energy would be required to get over the hill, assuming that amount of energy is even possible. Quantum tunneling; however, occurs without overcoming such a requisite energy threshold, going directly “through” the peak to the lower energy state. I’m not confident in my knowledge of quantum physics to attempt to explain further. Suffice to say, the occurrence of quantum tunneling does occur with certain probability. This probability is relatively small and decreases with increasing mass, hence the benefits of tunneling are typically only seen in quantum processes.
Real-world applications of quantum computing are starting to show up in press. Here is a recent one published by Volkswagen used to perform traffic optimization – note they used D-Wave.
Volkswagen AG has successfully demonstrated the world’s first live use of quantum computing to help optimize traffic routing. During the Web Summit conference in Lisbon, Portugal, nine public transit buses used a traffic management system developed by Volkswagen scientists in the United States and Germany, powered by a D-Wave quantum computer, to calculate the fastest travel routes individually and in near-real time.
D-Wave’s annealing systems are now also available through the recently announced ‘Braket’ service by Amazon (a play on ‘ket’ notation in quantum computing). In addition to D-Wave, Amazon Braket also front-ends IonQ and Rigetti quantum services. In should be noted that Jeff Bezos is an early investor in D-Wave (2012), and Amazon is also an investor in IonQ. IonQ uses a trapped ion modality (qubit physical architecture) approach to gate-model quantum computing, unlike superconducting qubits used by IBM Q and Google. One can see the investment by Amazon in technologies competitive to other big players. I’ve yet to research Rigetti and will add an addendum at some point.
Summary: Quantum computing continues to present new levels of learning, starting with basic qubit behavior & concepts. Beyond that, it is important to understand that there are more than one way to leverage qubits and quantum properties – gate-model and annealing being the leading methodologies.
Thanks for reading! Here’s a list of resources used in the pre-reading for this post:
- D-Wave Intro to Quantum Annealing Video Series: (Each of these is about 6 minutes – WATCH THEM!)
- Quantum Tunneling Intro: (Each of these is short, <2min)
- In-depth Tech Talk by Google: (~50min)


One thought on “What About Quantum Annealing? Amazon’s new ‘Braket’ service?”