Hi, everyone. It’s been a few months since my last post; my reason is that I’ve been working in the background to get some real, working knowledge behind this blog by completing some online training – the Quantum Computing Fundamentals course offered online through MITx PRO. My short review is: while it came at a pricey cost, it was well worth the investment in terms of the level of depth, hands on programming experience, and breadth of concepts taught. This takes us, somewhat indirectly, to today’s topic: what do all the hype articles mean when they same quantum bits (“qubits”) are unique from classical bits because they are capable of being “zero and one at the same time”.

Related to this, you’ll typically hear this phrase as the short-hand explanation of the term superposition. Here’s a few examples:
-
Quantum Computing for the Qubit Curious “Quantum computing relies on quantum bits, or “qubits”, which can also represent a 0 or a 1. The crazy thing is, qubits can also achieve a mixed state, called a “superposition” where they are both 1 and 0 at the same time.”
-
Quantum What? The Future of Computing and Electronics Is All About Qubits “You can think of a qubit as the equivalent to the classic bits in modern computing, with a twist. Like bits, qubits are also measured using our binary system of 1s and 0s. But unlike a classical bit, qubits can be both a 1 and a 0 at the same time. It gets even stranger.”
-
How Quantum Computers Work: Defining the Quantum Computer “This means that the symbols on the tape can be either 0 or 1 or a superposition of 0 and 1; in other words the symbols are both 0 and 1 (and all points in between) at the same time.”
By the way, each of these articles is a solid introductory article – you should read each of them. In my experience, this notion of “zero and one at the same time” repeats itself in online coverage similar to these, seemingly as a way to build exciting around quantum computing. Of course, however, it should – it’s true…for the most part. After taking the online class, I found “0 and 1 at the same time” to be an overloaded term, so let’s go through.
Pause for the history: classical bits (built from semiconductor-based transistors, vacuum tubes, what have you) are the basis of modern electronics. They can hold a state of 0 or 1, on or off. That’s it, and it turns out you can do amazing things with 0 and 1. Now imagine something could be 0 or 1 at the same time, it’s not hard to imagine you could do way MORE amazing things. But how the heck is that possible?
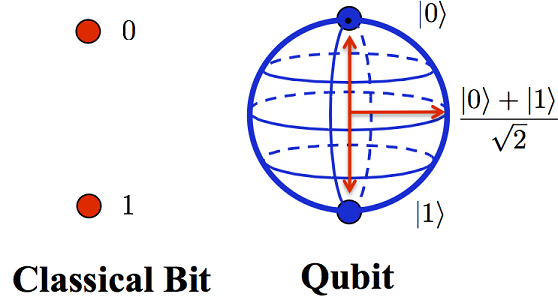
A qubit does have the notion of 0 and 1, but it also has the hard-to-grip concept of in-between. That’s what superposition is all about. To visualize that, we have to go back to an earlier article that introduced a theoretical visualization of a qubit, based on a sphere. This is formally called the Block Sphere. The state of a given qubit is expressed as it’s position on the sphere and better conceptualized as a vector than a simple 0 or 1 state.
The state at the top pole of the Block sphere is referred to as |0>, the state at the bottom pole as |1>, the state at the middle (not going into the math here) as (|0> + |1>) / √2. Voila!… 0 and 1 at the same time. It’s not so much that the qubit is in both states at the same time, it’s that it’s somewhere in between, or indeterminate.
Getting into the next phase of “interesting”, the fascinating potential of quantum computing is in it’s theoretical ability to leverage such indeterminate states to produce faster computations than classical computers (“quantum advantage”). Now that we have the means to create qubits (not too long ago we did not), the challenge of modern quantum computing is to find applications that leverage these properties. I haven’t yet identified a straight-forward enough example that I can illustrate in a blog post, but I’m working on it. As a near term alternative, I’ll at least demonstrate the effect of superposition, utilizing an online simulator.